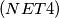
A boy has a set of trains and pieces of railroad track. Each piece is a quarter of circle, and by concatenating these pieces, the boy obtained a closed railway. The railway does not intersect itself. In passing through this railway, the train sometimes goes in the clockwise direction, and sometimes in the opposite direction. Prove that the train passes an even number of times through the pieces in the clockwise direction and an even number of times in the counterclockwise direction. Also, prove that the number of pieces is divisible by
%V0
$(NET 4)$ A boy has a set of trains and pieces of railroad track. Each piece is a quarter of circle, and by concatenating these pieces, the boy obtained a closed railway. The railway does not intersect itself. In passing through this railway, the train sometimes goes in the clockwise direction, and sometimes in the opposite direction. Prove that the train passes an even number of times through the pieces in the clockwise direction and an even number of times in the counterclockwise direction. Also, prove that the number of pieces is divisible by $4.$
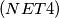 A boy has a set of trains and pieces of railroad track. Each piece is a quarter of circle, and by concatenating these pieces, the boy obtained a closed railway. The railway does not intersect itself. In passing through this railway, the train sometimes goes in the clockwise direction, and sometimes in the opposite direction. Prove that the train passes an even number of times through the pieces in the clockwise direction and an even number of times in the counterclockwise direction. Also, prove that the number of pieces is divisible by
A boy has a set of trains and pieces of railroad track. Each piece is a quarter of circle, and by concatenating these pieces, the boy obtained a closed railway. The railway does not intersect itself. In passing through this railway, the train sometimes goes in the clockwise direction, and sometimes in the opposite direction. Prove that the train passes an even number of times through the pieces in the clockwise direction and an even number of times in the counterclockwise direction. Also, prove that the number of pieces is divisible by 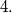
 Školjka
Školjka