Ako za trokute s duljinama stranica

,

,

i
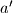
,
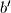
,
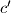
te nasuprotnim kutovima

,

,

i
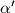
,
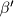
,
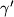
vrijede jednakosti
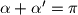
i
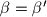
, dokažite da vrijedi i jednakost
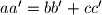
.
%V0
Ako za trokute s duljinama stranica $a$, $b$, $c$ i $a^\prime$, $b^\prime$, $c^\prime$ te nasuprotnim kutovima $\alpha$, $\beta$, $\gamma$ i $\alpha^\prime$, $\beta^\prime$, $\gamma^\prime$ vrijede jednakosti $\alpha + \alpha^\prime = \pi$ i $\beta = \beta^\prime$, dokažite da vrijedi i jednakost $aa^\prime = bb^\prime + cc^\prime$.