Let
and
be two natural numbers that have an equal number
of digits in their decimal expansions. The first
digits (from left to right) of the numbers
and
are equal. Prove that if
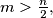
then
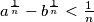
%V0
Let $a$ and $b$ be two natural numbers that have an equal number $n$ of digits in their decimal expansions. The first $m$ digits (from left to right) of the numbers $a$ and $b$ are equal. Prove that if $m >\frac{n}{2},$ then $a^{\frac{1}{n}} -b^{\frac{1}{n}} <\frac{1}{n}$
Školjka