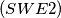
For each
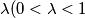
and
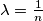
for all
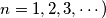
, construct a continuous function

such that there do not exist
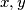
with
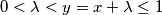
for which
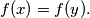
%V0
$(SWE 2)$ For each $\lambda (0 < \lambda < 1$ and $\lambda = \frac{1}{n}$ for all $n = 1, 2, 3, \cdots)$, construct a continuous function $f$ such that there do not exist $x, y$ with $0 < \lambda < y = x + \lambda \le 1$ for which $f(x) = f(y).$