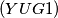
Suppose that positive real numbers
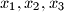
satisfy
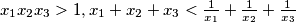
Prove that:
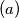
None of
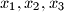
equals

.
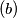
Exactly one of these numbers is less than
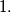
%V0
$(YUG 1)$ Suppose that positive real numbers $x_1, x_2, x_3$ satisfy
$x_1x_2x_3 > 1, x_1 + x_2 + x_3 <\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}$
Prove that:
$(a)$ None of $x_1, x_2, x_3$ equals $1$.
$(b)$ Exactly one of these numbers is less than $1.$