Let

be an interior point of the tetrahedron

. Prove that
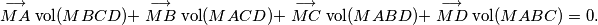
(
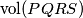
denotes the volume of the tetrahedron
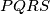
).
%V0
Let $M$ be an interior point of the tetrahedron $ABCD$. Prove that $$\stackrel{\longrightarrow }{MA} \text{vol}(MBCD) + \stackrel{\longrightarrow }{MB} \text{vol}(MACD) + \stackrel{\longrightarrow }{MC} \text{vol}(MABD) + \stackrel{\longrightarrow }{MD} \text{vol}(MABC) = 0\text{.}$$
($\text{vol}(PQRS)$ denotes the volume of the tetrahedron $PQRS$).