Slični zadaci
Let  be an acute-angled triangle. The lines
be an acute-angled triangle. The lines 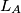 ,
, 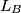 and
and 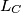 are constructed through the vertices
are constructed through the vertices  ,
,  and
and  respectively according the following prescription: Let
respectively according the following prescription: Let  be the foot of the altitude drawn from the vertex
be the foot of the altitude drawn from the vertex  to the side
to the side  ; let
; let 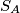 be the circle with diameter
be the circle with diameter 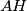 ; let
; let 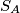 meet the sides
meet the sides  and
and  at
at  and
and  respectively, where
respectively, where  and
and  are distinct from
are distinct from  ; then let
; then let 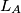 be the line through
be the line through  perpendicular to
perpendicular to  . The lines
. The lines 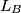 and
and 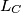 are constructed similarly. Prove that the lines
are constructed similarly. Prove that the lines 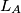 ,
, 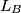 and
and 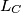 are concurrent.
are concurrent.
 be an acute-angled triangle. The lines
be an acute-angled triangle. The lines 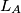 ,
, 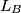 and
and 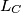 are constructed through the vertices
are constructed through the vertices  ,
,  and
and  respectively according the following prescription: Let
respectively according the following prescription: Let  be the foot of the altitude drawn from the vertex
be the foot of the altitude drawn from the vertex  to the side
to the side  ; let
; let 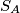 be the circle with diameter
be the circle with diameter 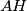 ; let
; let 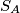 meet the sides
meet the sides  and
and  at
at  and
and  respectively, where
respectively, where  and
and  are distinct from
are distinct from  ; then let
; then let 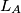 be the line through
be the line through  perpendicular to
perpendicular to  . The lines
. The lines 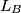 and
and 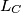 are constructed similarly. Prove that the lines
are constructed similarly. Prove that the lines 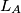 ,
, 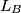 and
and 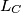 are concurrent.
are concurrent. Let  be a convex quadrilateral whose vertices do not lie on a circle. Let
be a convex quadrilateral whose vertices do not lie on a circle. Let 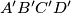 be a quadrangle such that
be a quadrangle such that 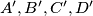 are the centers of the circumcircles of triangles
are the centers of the circumcircles of triangles 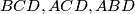 , and
, and  . We write
. We write 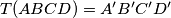 . Let us define
. Let us define 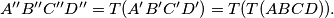
(a) Prove that and
and 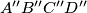 are similar.
are similar.
(b) The ratio of similitude depends on the size of the angles of . Determine this ratio.
. Determine this ratio.
 be a convex quadrilateral whose vertices do not lie on a circle. Let
be a convex quadrilateral whose vertices do not lie on a circle. Let 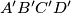 be a quadrangle such that
be a quadrangle such that 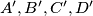 are the centers of the circumcircles of triangles
are the centers of the circumcircles of triangles 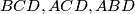 , and
, and  . We write
. We write 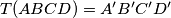 . Let us define
. Let us define 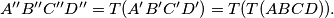
(a) Prove that
 and
and 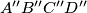 are similar.
are similar.(b) The ratio of similitude depends on the size of the angles of
 . Determine this ratio.
. Determine this ratio.  Školjka
Školjka 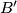 and
and 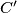 be the midpoints of the sides
be the midpoints of the sides 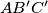 ,
,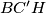 , and
, and 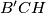 have a common point
have a common point  and that the line
and that the line 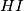 passes through the midpoint of the segment
passes through the midpoint of the segment 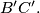
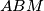 and
and 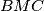 are equal. Prove that
are equal. Prove that 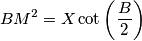

 be the centre of the inscribed circle of a triangle
be the centre of the inscribed circle of a triangle 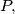
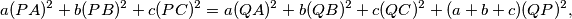
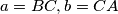 and
and 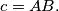
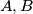 and
and 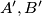 and
and 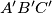 is greater than or equal to the area of triangle
is greater than or equal to the area of triangle 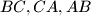 in
in 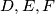 , respectively, and
, respectively, and 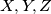 are the midpoints of
are the midpoints of 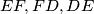 , respectively. Prove that the centers of the inscribed circle and of the circles around
, respectively. Prove that the centers of the inscribed circle and of the circles around 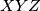 and
and