Consider a sequence of circles 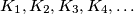 of radii
of radii 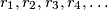 , respectively, situated inside a triangle
, respectively, situated inside a triangle  . The circle
. The circle 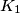 is tangent to
is tangent to  and
and  ;
; 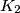 is tangent to
is tangent to 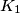 ,
, 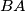 , and
, and  ;
; 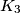 is tangent to
is tangent to 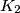 ,
,  , and
, and 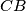 ;
; 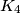 is tangent to
is tangent to 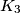 ,
,  , and
, and  ; etc.
; etc.
(a) Prove the relation
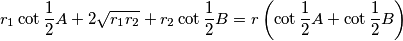
where is the radius of the incircle of the triangle
is the radius of the incircle of the triangle  . Deduce the existence of a
. Deduce the existence of a 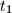 such that
such that
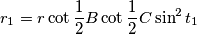
(b) Prove that the sequence of circles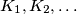 is periodic.
is periodic.
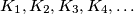 of radii
of radii 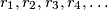 , respectively, situated inside a triangle
, respectively, situated inside a triangle  . The circle
. The circle 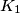 is tangent to
is tangent to  and
and  ;
; 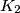 is tangent to
is tangent to 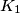 ,
, 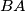 , and
, and  ;
; 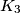 is tangent to
is tangent to 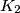 ,
,  , and
, and 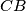 ;
; 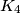 is tangent to
is tangent to 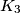 ,
,  , and
, and  ; etc.
; etc. (a) Prove the relation
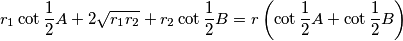
where
 is the radius of the incircle of the triangle
is the radius of the incircle of the triangle  . Deduce the existence of a
. Deduce the existence of a 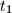 such that
such that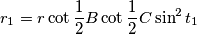
(b) Prove that the sequence of circles
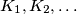 is periodic.
is periodic.  Školjka
Školjka