Establish if there exists a finite set

of points in space, not all situated in the same plane, so that for any straight line

which contains at least two points from M there exists another straight line
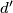
, parallel with
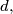
but distinct from

, which also contains at least two points from

.
%V0
Establish if there exists a finite set $M$ of points in space, not all situated in the same plane, so that for any straight line $d$ which contains at least two points from M there exists another straight line $d'$, parallel with $d,$ but distinct from $d$, which also contains at least two points from $M$.