Slični zadaci
Three faces of a tetrahedron are right triangles, while the fourth is not an obtuse triangle.
(a) Prove that a necessary and sufficient condition for the fourth face to be a right triangle is that at some vertex exactly two angles are right.
(b) Prove that if all the faces are right triangles, then the volume of the tetrahedron equals one -sixth the product of the three smallest edges not belonging to the same face.
(a) Prove that a necessary and sufficient condition for the fourth face to be a right triangle is that at some vertex exactly two angles are right.
(b) Prove that if all the faces are right triangles, then the volume of the tetrahedron equals one -sixth the product of the three smallest edges not belonging to the same face.
 Školjka
Školjka  , let
, let 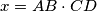 ,
, 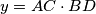 , and
, and 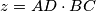 . Prove that there exists a triangle with edges
. Prove that there exists a triangle with edges 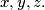
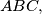 let
let 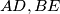 be altitudes and
be altitudes and 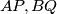 internal bisectors. Denote by
internal bisectors. Denote by  and
and  the incenter and the circumcentre of the triangle, respectively. Prove that the points
the incenter and the circumcentre of the triangle, respectively. Prove that the points 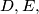 and
and 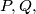 and
and 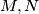 distinct points in the planes
distinct points in the planes  and
and 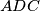 respectively. Show that the segments
respectively. Show that the segments 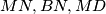 are the sides of a triangle.
are the sides of a triangle. 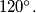
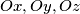 be three rays, and
be three rays, and  a point inside the trihedron
a point inside the trihedron 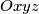 . Consider all planes passing through
. Consider all planes passing through  , respectively. How is the plane to be placed in order to yield a tetrahedron
, respectively. How is the plane to be placed in order to yield a tetrahedron 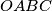 with minimal perimeter ?
with minimal perimeter ?