Let
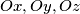
be three rays, and

a point inside the trihedron
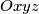
. Consider all planes passing through

and cutting
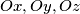
at points

, respectively. How is the plane to be placed in order to yield a tetrahedron
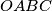
with minimal perimeter ?
%V0
Let $Ox, Oy, Oz$ be three rays, and $G$ a point inside the trihedron $Oxyz$. Consider all planes passing through $G$ and cutting $Ox, Oy, Oz$ at points $A,B,C$, respectively. How is the plane to be placed in order to yield a tetrahedron $OABC$ with minimal perimeter ?