The sum of the squares of five real numbers
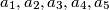
equals

. Prove that the least of the numbers
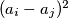
, where
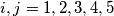
and
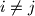
, does not exceed
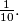
%V0
The sum of the squares of five real numbers $a_1, a_2, a_3, a_4, a_5$ equals $1$. Prove that the least of the numbers $(a_i - a_j)^2$, where $i, j = 1, 2, 3, 4,5$ and $i \neq j$, does not exceed $\frac{1}{10}.$