Let
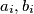
be coprime positive integers for
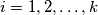
, and

the least common multiple of
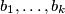
. Prove that the greatest common divisor of
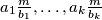
equals the greatest common divisor of
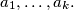
%V0
Let $a_i, b_i$ be coprime positive integers for $i = 1, 2, \ldots , k$, and $m$ the least common multiple of $b_1, \ldots , b_k$. Prove that the greatest common divisor of $a_1 \frac{m}{b_1} , \ldots, a_k \frac{m}{b_k}$ equals the greatest common divisor of $a_1, \ldots , a_k.$