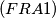
Let

and

be two nonnegative integers. Denote by
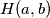
the set of numbers

of the form
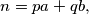
where

and
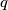
are positive integers. Determine
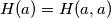
. Prove that if
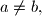
it is enough to know all the sets
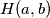
for coprime numbers
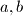
in order to know all the sets
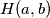
. Prove that in the case of coprime numbers

and
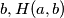
contains all numbers greater than or equal to
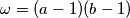
and also
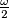
numbers smaller than
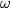
%V0
$(FRA 1)$ Let $a$ and $b$ be two nonnegative integers. Denote by $H(a, b)$ the set of numbers $n$ of the form $n = pa + qb,$ where $p$ and $q$ are positive integers. Determine $H(a) = H(a, a)$. Prove that if $a \neq b,$ it is enough to know all the sets $H(a, b)$ for coprime numbers $a, b$ in order to know all the sets $H(a, b)$. Prove that in the case of coprime numbers $a$ and $b, H(a, b)$ contains all numbers greater than or equal to $\omega = (a - 1)(b -1)$ and also $\frac{\omega}{2}$ numbers smaller than $\omega$
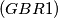 The polynomial
The polynomial 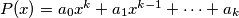 , where
, where 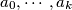 are integers, is said to be divisible by an integer
are integers, is said to be divisible by an integer  if
if 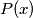 is a multiple of
is a multiple of  for every integral value of
for every integral value of  . Show that if
. Show that if 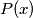 is divisible by
is divisible by  , then
, then 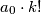 is a multiple of
is a multiple of  . Also prove that if
. Also prove that if 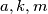 are positive integers such that
are positive integers such that 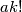 is a multiple of
is a multiple of  , then a polynomial
, then a polynomial 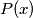 with leading term
with leading term 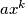 can be found that is divisible by
can be found that is divisible by 
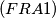 Let
Let  and
and  be two nonnegative integers. Denote by
be two nonnegative integers. Denote by 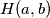 the set of numbers
the set of numbers  of the form
of the form 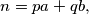 where
where  and
and 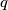 are positive integers. Determine
are positive integers. Determine 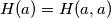 . Prove that if
. Prove that if 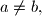 it is enough to know all the sets
it is enough to know all the sets 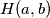 for coprime numbers
for coprime numbers 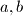 in order to know all the sets
in order to know all the sets 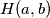 . Prove that in the case of coprime numbers
. Prove that in the case of coprime numbers  and
and 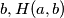 contains all numbers greater than or equal to
contains all numbers greater than or equal to 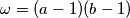 and also
and also 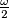 numbers smaller than
numbers smaller than 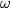
 Školjka
Školjka 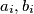 be coprime positive integers for
be coprime positive integers for 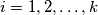 , and
, and 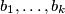 . Prove that the greatest common divisor of
. Prove that the greatest common divisor of 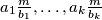 equals the greatest common divisor of
equals the greatest common divisor of 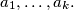
 Let
Let 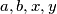 be positive integers such that
be positive integers such that 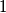 . Prove that the largest number not expressible in the form
. Prove that the largest number not expressible in the form 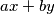 is
is 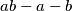 . If
. If 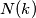 is the largest number not expressible in the form
is the largest number not expressible in the form  ways, find
ways, find 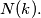
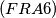 Consider the integer
Consider the integer 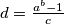 , where
, where  are positive integers and
are positive integers and 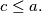 Prove that the set
Prove that the set 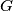 of integers that are between
of integers that are between  and relatively prime to
and relatively prime to 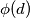 ) can be partitioned into
) can be partitioned into 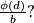
 Let
Let 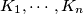 be nonnegative integers. Prove that
be nonnegative integers. Prove that ![K_1!K_2!\cdots K_n! \ge \left[\frac{K}{n}\right]!^n](/media/m/5/7/f/57fc388117dce24e551c1afc1962f1a9.png) , where
, where 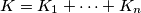
 Let
Let 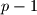 natural numbers
natural numbers 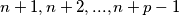 such that the sum of the squares of these numbers is divisible by the sum of these numbers?
such that the sum of the squares of these numbers is divisible by the sum of these numbers?