Let  be a triangle. Prove that there exists a point
be a triangle. Prove that there exists a point  on the side
on the side  of the triangle
of the triangle  , such that
, such that  is the geometric mean of
is the geometric mean of  and
and 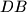 , iff the triangle
, iff the triangle  satisfies the inequality
satisfies the inequality 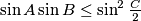 .
.
CommentAlternative formulation, from IMO ShortList 1974, Finland 2: We consider a triangle . Prove that:
. Prove that: 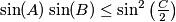 is a necessary and sufficient condition for the existence of a point
is a necessary and sufficient condition for the existence of a point  on the segment
on the segment  so that
so that  is the geometrical mean of
is the geometrical mean of  and
and  .
.
 be a triangle. Prove that there exists a point
be a triangle. Prove that there exists a point  on the side
on the side  of the triangle
of the triangle  , such that
, such that  is the geometric mean of
is the geometric mean of  and
and 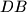 , iff the triangle
, iff the triangle  satisfies the inequality
satisfies the inequality 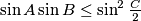 .
. CommentAlternative formulation, from IMO ShortList 1974, Finland 2: We consider a triangle
 . Prove that:
. Prove that: 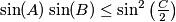 is a necessary and sufficient condition for the existence of a point
is a necessary and sufficient condition for the existence of a point  on the segment
on the segment  so that
so that  is the geometrical mean of
is the geometrical mean of  and
and  .
.  Školjka
Školjka