We consider the division of a chess board 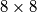 in p disjoint rectangles which satisfy the conditions:
in p disjoint rectangles which satisfy the conditions:
a) every rectangle is formed from a number of full squares (not partial) from the 64 and the number of white squares is equal to the number of black squares.
b) the numbers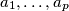 of white squares from
of white squares from  rectangles satisfy
rectangles satisfy 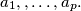 Find the greatest value of
Find the greatest value of  for which there exists such a division and then for that value of
for which there exists such a division and then for that value of 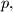 all the sequences
all the sequences 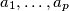 for which we can have such a division.
for which we can have such a division.
Moderator says: see http://www.artofproblemsolving.com/Foru ... 41t=58591
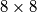 in p disjoint rectangles which satisfy the conditions:
in p disjoint rectangles which satisfy the conditions:a) every rectangle is formed from a number of full squares (not partial) from the 64 and the number of white squares is equal to the number of black squares.
b) the numbers
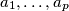 of white squares from
of white squares from  rectangles satisfy
rectangles satisfy 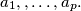 Find the greatest value of
Find the greatest value of  for which there exists such a division and then for that value of
for which there exists such a division and then for that value of 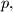 all the sequences
all the sequences 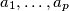 for which we can have such a division.
for which we can have such a division.Moderator says: see http://www.artofproblemsolving.com/Foru ... 41t=58591
 Školjka
Školjka