We consider two sequences of real numbers
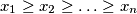
and
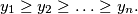
Let
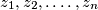
be a permutation of the numbers
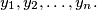
Prove that
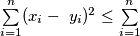
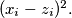
%V0
We consider two sequences of real numbers $x_{1} \geq x_{2} \geq \ldots \geq x_{n}$ and $\ y_{1} \geq y_{2} \geq \ldots \geq y_{n}.$ Let $z_{1}, z_{2}, .\ldots, z_{n}$ be a permutation of the numbers $y_{1}, y_{2}, \ldots, y_{n}.$ Prove that $\sum \limits_{i=1}^{n} ( x_{i} -\ y_{i} )^{2} \leq \sum \limits_{i=1}^{n}$ $( x_{i} - z_{i})^{2}.$