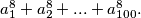Slični zadaci
There are six ports on a lake. Is it possible to organize a series of routes satisfying the following conditions ?
(i) Every route includes exactly three ports;
(ii) No two routes contain the same three ports;
(iii) The series offers exactly two routes to each tourist who desires to visit two different arbitrary ports.
(i) Every route includes exactly three ports;
(ii) No two routes contain the same three ports;
(iii) The series offers exactly two routes to each tourist who desires to visit two different arbitrary ports.
 Školjka
Školjka ![\left[ \sum_{n=1}^{10^9} n^{-2/3} \right]](/media/m/6/8/4/684c8c9458d9b87753898dbd5d5ddbdb.png) . Here
. Here ![[x]](/media/m/6/a/4/6a47dfb91475b9d5490dbb3a666604a3.png) denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to 
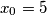 and
and 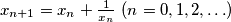 . Prove that
. Prove that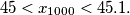
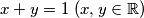 it follows that
it follows that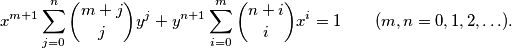
 points
points 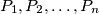 are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance
are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance  between any two of these points has its largest possible value
between any two of these points has its largest possible value 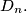 Calculate
Calculate 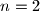 to 7. and justify your answer.
to 7. and justify your answer. 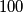 (or
(or 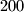 ) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer.
) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer. 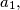
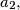
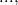
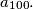 Determine the last two digits of the number
Determine the last two digits of the number