Let
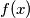
be a continuous function defined on the closed interval
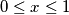
. Let
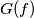
denote the graph of
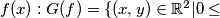
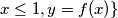
. Let
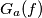
denote the graph of the translated function
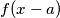
(translated over a distance

), defined by
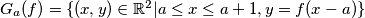
. Is it possible to find for every
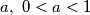
, a continuous function
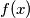
, defined on
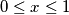
, such that
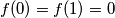
and
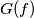
and
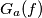
are disjoint point sets ?
%V0
Let $f(x)$ be a continuous function defined on the closed interval $0 \leq x \leq 1$. Let $G(f)$ denote the graph of $f(x): G(f) = \{(x, y) \in \mathbb R^2 | 0 \leq$ $x \leq 1, y = f(x) \}$. Let $G_a(f)$ denote the graph of the translated function $f(x - a)$ (translated over a distance $a$), defined by $G_a(f) = \{(x, y) \in \mathbb R^2 | a \leq x \leq a + 1, y = f(x - a) \}$. Is it possible to find for every $a, \ 0 < a < 1$, a continuous function $f(x)$, defined on $0 \leq x \leq 1$, such that $f(0) = f(1) = 0$ and $G(f)$ and $G_a(f)$ are disjoint point sets ?