Can there be drawn on a circle of radius
a number of
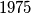
distinct points, so that the distance (measured on the chord) between any two points (from the considered points) is a rational number?
%V0
Can there be drawn on a circle of radius $1$ a number of $1975$ distinct points, so that the distance (measured on the chord) between any two points (from the considered points) is a rational number?
Školjka