Let

be a triangle with bisectors
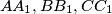
(
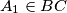
, etc.) and

their common point. Consider the triangles
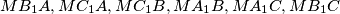
, and their inscribed circles. Prove that if four of these six inscribed circles have equal radii, then
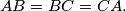
%V0
Let $ABC$ be a triangle with bisectors $AA_1,BB_1, CC_1$ ($A_1 \in BC$, etc.) and $M$ their common point. Consider the triangles $MB_1A, MC_1A,MC_1B,MA_1B,MA_1C,MB_1C$, and their inscribed circles. Prove that if four of these six inscribed circles have equal radii, then $AB = BC = CA.$