We consider the following system with
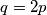
:
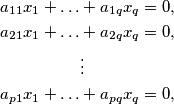
in which every coefficient is an element from the set
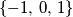

Prove that there exists a solution
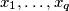
for the system with the properties:
a.) all
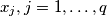
are integers;
b.) there exists at least one j for which
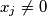
;
c.)
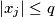
for any
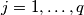
.
%V0
We consider the following system with $q=2p$: $$$\begin{align*}
a_{11}x_{1}+\ldots&+a_{1q}x_{q}=0,\\
a_{21}x_{1}+\ldots&+a_{2q}x_{q}=0,\\
&\vdots \\
a_{p1}x_{1}+\ldots&+a_{pq}x_{q}=0,\\
\end{align*}$$$ in which every coefficient is an element from the set $\{-1,\,0,\,1\}$ $.$ Prove that there exists a solution $x_{1}, \ldots, x_{q}$ for the system with the properties:
a.) all $x_{j}, j=1,\ldots,q$ are integers;
b.) there exists at least one j for which $x_{j} \neq 0$;
c.) $|x_{j}| \leq q$ for any $j=1, \ldots ,q$.