There are 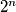 words of length
words of length  over the alphabet
over the alphabet 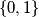 . Prove that the following algorithm generates the sequence
. Prove that the following algorithm generates the sequence 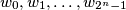 of all these words such that any two consecutive words differ in exactly one digit.
of all these words such that any two consecutive words differ in exactly one digit.
(1)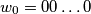 (
( zeros).
zeros).
(2) Suppose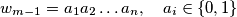 . Let
. Let 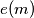 be the exponent of
be the exponent of  in the representation of
in the representation of  as a product of primes, and let
as a product of primes, and let 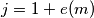 . Replace the digit
. Replace the digit 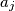 in the word
in the word  by
by 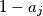 . The obtained word is
. The obtained word is 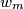 .
.
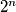 words of length
words of length  over the alphabet
over the alphabet 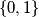 . Prove that the following algorithm generates the sequence
. Prove that the following algorithm generates the sequence 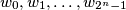 of all these words such that any two consecutive words differ in exactly one digit.
of all these words such that any two consecutive words differ in exactly one digit.(1)
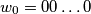 (
( zeros).
zeros).(2) Suppose
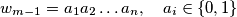 . Let
. Let 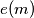 be the exponent of
be the exponent of  in the representation of
in the representation of  as a product of primes, and let
as a product of primes, and let 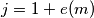 . Replace the digit
. Replace the digit 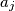 in the word
in the word  by
by 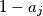 . The obtained word is
. The obtained word is 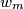 .
.  Školjka
Školjka