Let
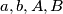
be given reals. We consider the function defined by
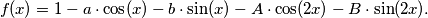
Prove that if for any real number

we have
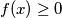
then
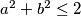
and
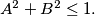
%V0
Let $a,b,A,B$ be given reals. We consider the function defined by $$f(x) = 1 - a \cdot \cos(x) - b \cdot \sin(x) - A \cdot \cos(2x) - B \cdot \sin(2x).$$ Prove that if for any real number $x$ we have $f(x) \geq 0$ then $a^2 + b^2 \leq 2$ and $A^2 + B^2 \leq 1.$