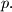Slični zadaci
A figure with area  is cut out of paper. We divide this figure into
is cut out of paper. We divide this figure into  parts and color them in
parts and color them in  different colors. Now, we turn around the piece of paper, divide the same figure on the other side of the paper in
different colors. Now, we turn around the piece of paper, divide the same figure on the other side of the paper in  parts again (in some different way). Show that we can color these new parts in the same
parts again (in some different way). Show that we can color these new parts in the same  colors again (hereby, different parts should have different colors) such that the sum of the areas of all parts of the figure colored with the same color on both sides is
colors again (hereby, different parts should have different colors) such that the sum of the areas of all parts of the figure colored with the same color on both sides is 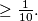
 is cut out of paper. We divide this figure into
is cut out of paper. We divide this figure into  parts and color them in
parts and color them in  different colors. Now, we turn around the piece of paper, divide the same figure on the other side of the paper in
different colors. Now, we turn around the piece of paper, divide the same figure on the other side of the paper in  parts again (in some different way). Show that we can color these new parts in the same
parts again (in some different way). Show that we can color these new parts in the same  colors again (hereby, different parts should have different colors) such that the sum of the areas of all parts of the figure colored with the same color on both sides is
colors again (hereby, different parts should have different colors) such that the sum of the areas of all parts of the figure colored with the same color on both sides is 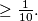
Consider  students with numbers
students with numbers 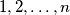 standing in the order
standing in the order 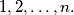 Upon a command, any of the students either remains on his place or switches his place with another student. (Actually, if student
Upon a command, any of the students either remains on his place or switches his place with another student. (Actually, if student  switches his place with student
switches his place with student  then
then  cannot switch his place with any other student
cannot switch his place with any other student  any more until the next command comes.)
any more until the next command comes.)
Is it possible to arrange the students in the order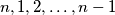 after two commands ?
after two commands ?
 students with numbers
students with numbers 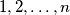 standing in the order
standing in the order 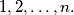 Upon a command, any of the students either remains on his place or switches his place with another student. (Actually, if student
Upon a command, any of the students either remains on his place or switches his place with another student. (Actually, if student  switches his place with student
switches his place with student  then
then  cannot switch his place with any other student
cannot switch his place with any other student  any more until the next command comes.)
any more until the next command comes.)Is it possible to arrange the students in the order
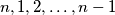 after two commands ?
after two commands ?  Školjka
Školjka ![x_1 = n, y_1 = 1, x_{i+1} =\left[ \frac{x_i+y_i}{2}\right] , y_{i+1} = \left[ \frac{n}{x_{i+1}}\right], \qquad \text{for }i =...](/media/m/8/0/2/80297c16d4034850b8005614863d0012.png)
![[z]](/media/m/1/b/e/1be90bc55017944743736332d25924af.png) denotes the largest integer less than or equal to
denotes the largest integer less than or equal to  . Prove that
. Prove that![\min \{x_1, x_2, \ldots, x_n \} =[ \sqrt n ]](/media/m/a/4/e/a4e6b4231171a1d8c8a4bfba6f520b36.png)
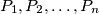 are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance
are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance 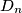 between any two of these points has its largest possible value
between any two of these points has its largest possible value 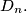 Calculate
Calculate 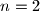 to 7. and justify your answer.
to 7. and justify your answer. 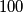 (or
(or 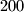 ) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer.
) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer. 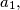
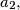
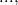
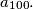 Determine the last two digits of the number
Determine the last two digits of the number 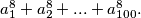
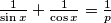 where
where  is a real parameter.
is a real parameter. for a given
for a given