Neka su

,

,

realni brojevi,
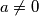
. Ako je

jedno rješenje jednadžbe
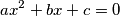
i
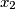
jedno rješenje jednadžbe
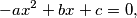
dokažite da je tada jedno rješenje
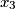
jednadžbe
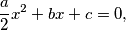
između

i
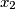
, tj.
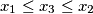
ili
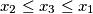
.
%V0
Neka su $a$, $b$, $c$ realni brojevi, $a \not= 0$. Ako je $x_1$ jedno rješenje jednadžbe $$ax^2 + bx + c = 0$$ i $x_2$ jedno rješenje jednadžbe $$-ax^2 + bx + c = 0\text{,}$$ dokažite da je tada jedno rješenje $x_3$ jednadžbe $$\frac{a}{2}x^2 + bx + c = 0\text{,}$$ između $x_1$ i $x_2$, tj. $x_1 \leq x_3 \leq x_2$ ili $x_2 \leq x_3 \leq x_1$.