Let

and

be positive integers such that
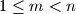
. In their decimal representations, the last three digits of
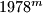
are equal, respectively, so the last three digits of
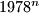
. Find

and

such that
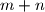
has its least value.
%V0
Let $m$ and $n$ be positive integers such that $1 \le m < n$. In their decimal representations, the last three digits of $1978^m$ are equal, respectively, so the last three digits of $1978^n$. Find $m$ and $n$ such that $m + n$ has its least value.