For every integer
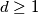
, let
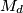
be the set of all positive integers that cannot be written as a sum of an arithmetic progression with difference

, having at least two terms and consisting of positive integers. Let
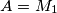
,
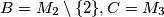
. Prove that every
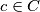
may be written in a unique way as
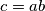
with
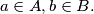
%V0
For every integer $d \geq 1$, let $M_d$ be the set of all positive integers that cannot be written as a sum of an arithmetic progression with difference $d$, having at least two terms and consisting of positive integers. Let $A = M_1$, $B = M_2 \setminus \{2 \}, C = M_3$. Prove that every $c \in C$ may be written in a unique way as $c = ab$ with $a \in A, b \in B.$