Let

be the set of all the odd positive integers that are not multiples of

and that are less than
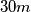
,

being an arbitrary positive integer. What is the smallest integer

such that in any subset of

integers from

there must be two different integers, one of which divides the other?
%V0
Let $S$ be the set of all the odd positive integers that are not multiples of $5$ and that are less than $30m$, $m$ being an arbitrary positive integer. What is the smallest integer $k$ such that in any subset of $k$ integers from $S$ there must be two different integers, one of which divides the other?