A function
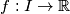
, defined on an interval

, is called concave if
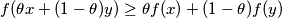
for all
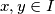
and
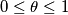
. Assume that the functions
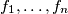
, having all nonnegative values, are concave. Prove that the function
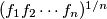
is concave.
%V0
A function $f : I \to \mathbb R$, defined on an interval $I$, is called concave if $f(\theta x + (1 - \theta)y) \geq \theta f(x) + (1 - \theta)f(y)$ for all $x, y \in I$ and $0 \leq \theta \leq 1$. Assume that the functions $f_1, \ldots , f_n$, having all nonnegative values, are concave. Prove that the function $(f_1f_2 \cdots f_n)^{1/n}$ is concave.