Školjka We consider a fixed point 
in the interior of a fixed sphere
We construct three segments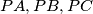 
, perpendicular two by two
with the vertexes 
on the sphere We consider the vertex 
which is opposite to in the parallelepiped (with right angles) with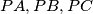 
as edges Find the locus of the point when take all the positions compatible with our problem.
in the interior of a fixed sphere We construct three segments 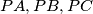, perpendicular two by two with the vertexes on the sphere We consider the vertex which is opposite to in the parallelepiped (with right angles) with 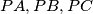as edges Find the locus of the point when take all the positions compatible with our problem.