Prove that it is possible to place
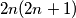
parallelepipedic (rectangular) pieces of soap of dimensions
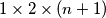
in a cubic box with edge
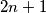
if and only if

is even or
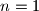
.
Remark. It is assumed that the edges of the pieces of soap are parallel to the edges of the box.
%V0
Prove that it is possible to place $2n(2n + 1)$ parallelepipedic (rectangular) pieces of soap of dimensions $1 \times 2 \times (n + 1)$ in a cubic box with edge $2n + 1$ if and only if $n$ is even or $n = 1$.
Remark. It is assumed that the edges of the pieces of soap are parallel to the edges of the box.