Prove that for any positive integers
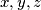
with
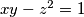
one can find non-negative integers
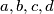
such that
.
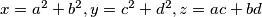
Set
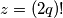
to deduce that for any prime number
,
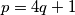
can be represented as the sum of squares of two integers.
%V0
Prove that for any positive integers $x, y, z$ with $xy-z^2 = 1$ one can find non-negative integers $a, b, c, d$ such that $x = a^2 + b^2, y = c^2 + d^2, z = ac + bd$.
Set $z = (2q)!$ to deduce that for any prime number $p = 4q + 1$, $p$ can be represented as the sum of squares of two integers.
Školjka