Let
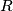
be a set of exactly
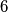
elements. A set

of subsets of
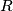
is called an

-family over
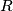
if and only if it satisfies the following three conditions:
(i) For no two sets
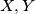
in

is
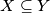
;
(ii) For any three sets
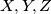
in

,
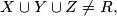
(iii)
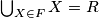
%V0
Let $R$ be a set of exactly $6$ elements. A set $F$ of subsets of $R$ is called an $S$-family over $R$ if and only if it satisfies the following three conditions:
(i) For no two sets $X, Y$ in $F$ is $X \subseteq Y$ ;
(ii) For any three sets $X, Y,Z$ in $F$, $X \cup Y \cup Z \neq R,$
(iii) $\bigcup_{X \in F} X = R$