Given the integer
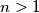
and the real number
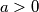
determine the maximum of
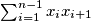
taken over all nonnegative numbers
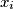
with sum
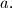
%V0
Given the integer $n > 1$ and the real number $a > 0$ determine the maximum of $\sum_{i=1}^{n-1} x_i x_{i+1}$ taken over all nonnegative numbers $x_i$ with sum $a.$