Prove that a convex pentagon (a five-sided polygon)
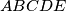
with equal sides and for which the interior angles satisfy the condition
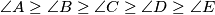
is a regular pentagon.
%V0
Prove that a convex pentagon (a five-sided polygon) $ABCDE$ with equal sides and for which the interior angles satisfy the condition $\angle A \geq \angle B \geq \angle C \geq \angle D \geq \angle E$ is a regular pentagon.