A finite set of unit circles is given in a plane such that the area of their union
is
. Prove that there exists a subset of mutually disjoint circles such that the area of their union is greater that
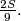
%V0
A finite set of unit circles is given in a plane such that the area of their union $U$ is $S$. Prove that there exists a subset of mutually disjoint circles such that the area of their union is greater that $\frac{2S}{9}.$
Školjka