Consider infinite sequences
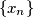
of positive reals such that
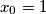
and
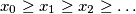
.
a) Prove that for every such sequence there is an
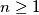
such that:
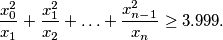
b) Find such a sequence such that for all

:
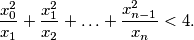
%V0
Consider infinite sequences $\{x_n\}$ of positive reals such that $x_0=1$ and $x_0\ge x_1\ge x_2\ge\ldots$.
a) Prove that for every such sequence there is an $n\ge1$ such that: $${x_0^2\over x_1}+{x_1^2\over x_2}+\ldots+{x_{n-1}^2\over x_n}\ge3.999.$$
b) Find such a sequence such that for all $n$: $${x_0^2\over x_1}+{x_1^2\over x_2}+\ldots+{x_{n-1}^2\over x_n}<4.$$