Let

be a positive integer. Let
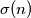
be the sum of the natural divisors

of

(including

and

). We say that an integer
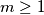
is superabundant (P.Erdos,
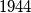
) if
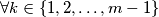
,
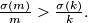
Prove that there exists an infinity of superabundant numbers.
%V0
Let $n$ be a positive integer. Let $\sigma(n)$ be the sum of the natural divisors $d$ of $n$ (including $1$ and $n$). We say that an integer $m \geq 1$ is superabundant (P.Erdos, $1944$) if $\forall k \in \{1, 2, \dots , m - 1 \}$, $\frac{\sigma(m)}{m} >\frac{\sigma(k)}{k}.$
Prove that there exists an infinity of superabundant numbers.