Let

be a positive integer and let
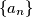
be defined by
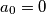
and
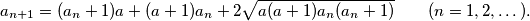
Show that for each positive integer

,

is a positive integer.
%V0
Let $a$ be a positive integer and let $\{a_n\}$ be defined by $a_0 = 0$ and
$$a_{n+1 }= (a_n + 1)a + (a + 1)a_n + 2 \sqrt{a(a + 1)a_n(a_n + 1)} \qquad (n = 1, 2 ,\dots ).$$
Show that for each positive integer $n$, $a_n$ is a positive integer.