In a test,
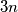
students participate, who are located in three rows of

students in each. The students leave the test room one by one. If
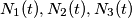
denote the numbers of students in the first, second, and third row respectively at time

, find the probability that for each t during the test,
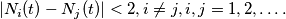
%V0
In a test, $3n$ students participate, who are located in three rows of $n$ students in each. The students leave the test room one by one. If $N_1(t), N_2(t), N_3(t)$ denote the numbers of students in the first, second, and third row respectively at time $t$, find the probability that for each t during the test,
$$|N_i(t) - N_j(t)| < 2, i \neq j, i, j = 1, 2, \dots .$$