Let
,
and
be the lengths of the sides of a triangle. Prove that
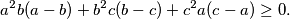
Determine when equality occurs.
%V0
Let $a$, $b$ and $c$ be the lengths of the sides of a triangle. Prove that
$$a^{2}b(a - b) + b^{2}c(b - c) + c^{2}a(c - a)\ge 0.$$
Determine when equality occurs.
Školjka