Let
and
be integers. Show that there exists an interval
of length
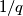
and a polynomial
with integral coefficients such that
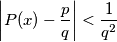
for all
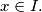
%V0
Let $p$ and $q$ be integers. Show that there exists an interval $I$ of length $1/q$ and a polynomial $P$ with integral coefficients such that
$$\left|P(x)-\frac pq \right| < \frac{1}{q^2}$$
for all $x \in I.$
Školjka