Is it possible to choose
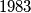
distinct positive integers, all less than or equal to
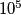
, no three of which are consecutive terms of an arithmetic progression?
%V0
Is it possible to choose $1983$ distinct positive integers, all less than or equal to $10^5$, no three of which are consecutive terms of an arithmetic progression?