Let
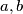
and

be positive integers, no two of which have a common divisor greater than
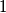
. Show that
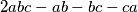
is the largest integer which cannot be expressed in the form
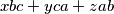
, where
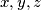
are non-negative integers.
%V0
Let $a,b$ and $c$ be positive integers, no two of which have a common divisor greater than $1$. Show that $2abc-ab-bc-ca$ is the largest integer which cannot be expressed in the form $xbc+yca+zab$, where $x,y,z$ are non-negative integers.