Let
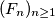
be the Fibonacci sequence
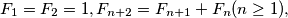
and
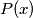
the polynomial of degree
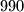
satisfying
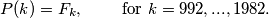
Prove that
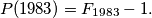
%V0
Let $(F_n)_{n\geq 1}$ be the Fibonacci sequence $F_1 = F_2 = 1, F_{n+2} = F_{n+1} + F_n (n \geq 1),$ and $P(x)$ the polynomial of degree $990$ satisfying
$$P(k) = F_k, \qquad \text{ for } k = 992, . . . , 1982.$$
Prove that $P(1983) = F_{1983} - 1.$