Let
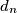
be the last nonzero digit of the decimal representation of
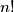
. Prove that
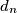
is aperiodic; that is, there do not exist
and
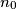
such that for all
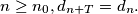
%V0
Let $d_n$ be the last nonzero digit of the decimal representation of $n!$. Prove that $d_n$ is aperiodic; that is, there do not exist $T$ and $n_0$ such that for all $n \geq n_0, d_{n+T} = d_n.$
Školjka