Let
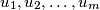
be

vectors in the plane, each of length
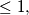
with zero sum. Show that one can arrange
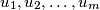
as a sequence
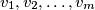
such that each partial sum
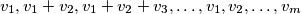
has length less than or equal to
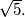
%V0
Let $u_1, u_2, \ldots, u_m$ be $m$ vectors in the plane, each of length $\leq 1,$ with zero sum. Show that one can arrange $u_1, u_2, \ldots, u_m$ as a sequence $v_1, v_2, \ldots, v_m$ such that each partial sum $v_1, v_1 + v_2, v_1 + v_2 + v_3, \ldots, v_1, v_2, \ldots, v_m$ has length less than or equal to $\sqrt {5}.$