Let
be a positive integer and
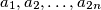
mutually distinct integers. Find all integers
satisfying
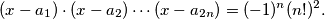
%V0
Let $n$ be a positive integer and $a_1, a_2, \dots , a_{2n}$ mutually distinct integers. Find all integers $x$ satisfying
$$(x - a_1) \cdot (x - a_2) \cdots (x - a_{2n}) = (-1)^n(n!)^2.$$
Školjka