In a permutation
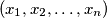
of the set
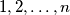
we call a pair
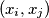
discordant if
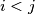
and
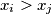
. Let
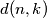
be the number of such permutations with exactly
discordant pairs. Find
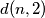
and
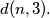
%V0
In a permutation $(x_1, x_2, \dots , x_n)$ of the set $1, 2, \dots , n$ we call a pair $(x_i, x_j )$ discordant if $i < j$ and $x_i > x_j$. Let $d(n, k)$ be the number of such permutations with exactly $k$ discordant pairs. Find $d(n, 2)$ and $d(n, 3).$
Školjka